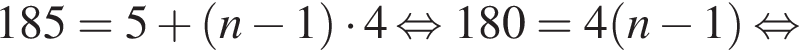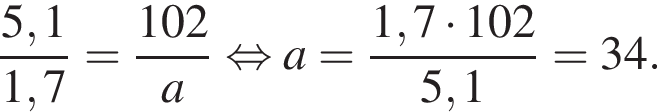Определите наименьшее натуральное число, кратное 2, которое при делении на 11 с остатком дает неполное частное, равное 5.
Функция 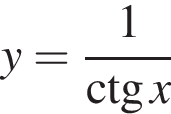 не определена в точке:
не определена в точке:
На рисунке изображен треугольник ABC, в котором ∠ACB = 41°, ∠AMN = 107°. Используя данные рисунка, найдите градусную меру угла BAC.
Укажите верное равенство:
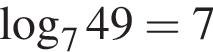
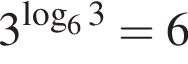
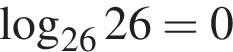
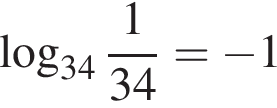

На клетчатой бумаге с клетками размером 1 см х 1 см изображён параллелограмм. Найдите его площадь в квадратных сантиметрах.
На рисунке изображен треугольник ABC, в котором ∠ACB = 37°, ∠AMN = 107°. Используя данные рисунка, найдите градусную меру угла BAC.
На рисунке изображен треугольник ABC, в котором ∠ACB = 32°, ∠AMN = 107°. Используя данные рисунка, найдите градусную меру угла BAC.
Запишите (5x)y в виде степени с основанием 5.
Пусть O и O1 — центры оснований цилиндра, изображенного на рисунке. Тогда образующей цилиндра является отрезок:
Пусть O и O1 — центры оснований цилиндра, изображенного на рисунке. Тогда образующей цилиндра является отрезок:
На клетчатой бумаге с клетками размером 1 см х 1 см изображён параллелограмм. Найдите его площадь в квадратных сантиметрах.
На клетчатой бумаге с клетками размером 1 см х 1 см изображён параллелограмм. Найдите его площадь в квадратных сантиметрах.
Укажите номер рисунка, на котором изображены фигуры, симметричные относительно прямой l.
Используя рисунок, определите верное утверждение и укажите его номер.
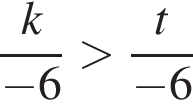


Найдите длину ребра правильной пятиугольной пирамиды, у которой боковое ребро равно ребру основания, а сумма длин всех ребер равна 30.
Сумма всех натуральных делителей числа 75 равна:
Сумма всех натуральных делителей числа 20 равна:
Арифметическая прогрессия (an) задана формулой n-го члена an = 6n + 1. Найдите разность этой прогрессии.
Сумма всех натуральных делителей числа 45 равна:
Среди точек
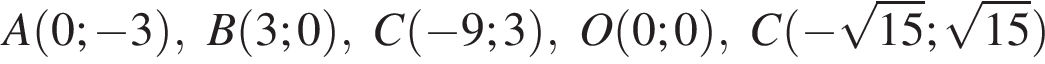 выберите ту, которая принадлежит графику функции, изображённому на рисунке:
выберите ту, которая принадлежит графику функции, изображённому на рисунке:
Среди точек
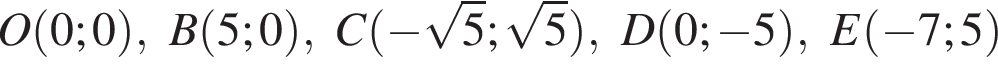 выберите ту, которая принадлежит графику функции, изображённому на рисунке:
выберите ту, которая принадлежит графику функции, изображённому на рисунке:
Арифметическая прогрессия (an) задана формулой n-го члена an = 5n − 2. Найдите разность этой прогрессии.
Прямые a и b, пересекаясь, образуют четыре угла. Известно, что сумма трех углов равна 210°. Найдите градусную меру меньшего угла.
Прямые a и b, пересекаясь, образуют четыре угла. Известно, что сумма трех углов равна 238°. Найдите градусную меру меньшего угла.
Значение выражения 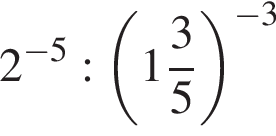 равно:
равно:
Результат разложения многочлена x (4a − b) + b − 4a на множители имеет вид:
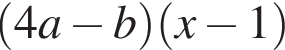
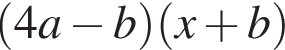
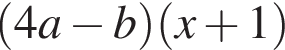
Если 18% некоторого числа равны 24, то 30% этого числа равны:
Если 18% некоторого числа равны 27, то 30% этого числа равны:
Укажите номер рисунка, на котором изображены фигуры, симметричные относительно точки O.
Если 16% некоторого числа равны 24, то 60% этого числа равны:
Результат разложения многочлена x (6a − b) + b − 6a на множители имеет вид:
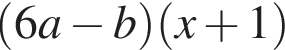
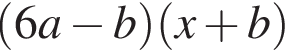
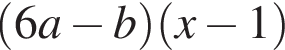
Даны квадратные уравнения:
Укажите уравнение, которое не имеет корней.
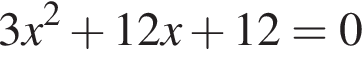
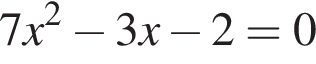
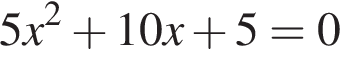
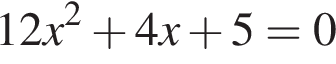
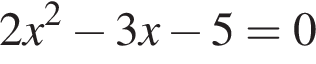
Результат разложения многочлена x (2a − b) + b − 2a на множители имеет вид:
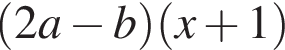
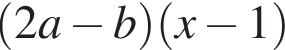
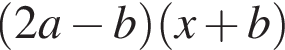
Укажите номер рисунка, на котором изображены фигуры, симметричные относительно точки O.
Укажите номер рисунка, на котором изображены фигуры, симметричные относительно точки O.
Число 125 является членом арифметической прогрессии 2, 5, 8, 11, ... Укажите его номер.
На рисунке изображены развернутый угол AOM и лучи OB и OC. Известно, что ∠AOC = 102°, ∠BOM = 128°. Найдите величину угла BOC.
Укажите номер рисунка, на котором показано множество решений системы неравенств 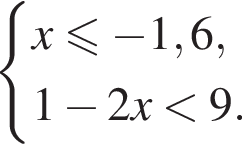
1)
2)
3)
4)
5)
Укажите номер рисунка, на котором показано множество решений системы неравенств 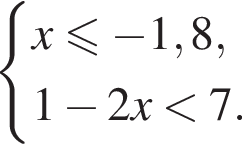
1)
2)
3)
4)
5)
Число 154 является членом арифметической прогрессии 4, 7, 10, 13, ... Укажите его номер.
На координатной плоскости изображен параллелограмм ABCD с вершинами в узлах сетки (см. рис.). Длина диагонали AC параллелограмма равна:
Число 213 является членом арифметической прогрессии 3, 8, 13, 18, ... Укажите его номер.
Результат упрощения выражения 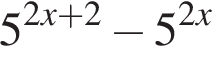 имеет вид:
имеет вид:
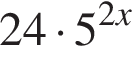
Величины a и b являются прямо пропорциональными. Используя данные таблицы, найдите неизвестное значение величины a.
| a | 1,3 | |
| b | 116 | 5,2 |
Результат упрощения выражения 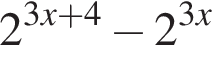 имеет вид:
имеет вид:
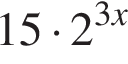
Результат упрощения выражения 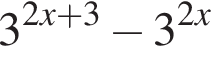 имеет вид:
имеет вид:
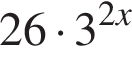
На координатной плоскости изображен параллелограмм ABCD с вершинами в узлах сетки (см.рис.). Длина диагонали BD параллелограмма равна:
Укажите номер рисунка, на котором показано множество решений системы неравенств 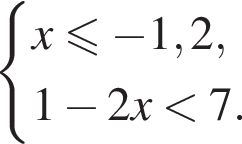
1)
2)
3)
4)
5)
На рисунке изображены развернутый угол AOM и лучи OB и OC. Известно, что
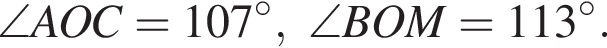 Найдите величину угла BOC.
Найдите величину угла BOC.
Укажите номер рисунка, на котором показано множество решений системы неравенств 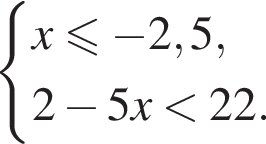
1)
2)
3)
4)
5)
Величины a и b являются прямо пропорциональными. Используя данные таблицы, найдите неизвестное значение величины a.
| a | 1,9 | |
| b | 108 | 7,6 |
На рисунке изображены развернутый угол AOM и лучи OB и OC. Известно, что ∠AOC = 144°, ∠BOM = 136°. Найдите величину угла BOC.
На координатной плоскости изображен параллелограмм ABCD с вершинами в узлах сетки (см.рис.). Длина диагонали AC параллелограмма равна:
Результат упрощения выражения 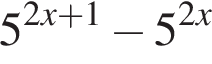 имеет вид:
имеет вид:
Результат упрощения выражения 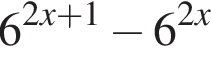 имеет вид:
имеет вид:
На рисунке изображены развернутый угол AOM и лучи OB и OC. Известно, что ∠AOC = 94°, ∠BOM = 126°. Найдите величину угла BOC.
Укажите номер рисунка, на котором показано множество решений системы неравенств 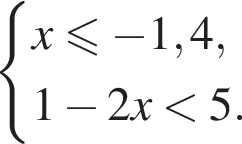
1)
2)
3)
4)
5)
На координатной плоскости изображен параллелограмм ABCD с вершинами в узлах сетки (см.рис.). Длина диагонали BD параллелограмма равна:
Число 133 является членом арифметической прогрессии 4, 7, 10, 13, ... Укажите его номер.
Величины a и b являются прямо пропорциональными. Используя данные таблицы, найдите неизвестное значение величины a.
| a | 2,9 | |
| b | 114 | 8,7 |
Найдите значение выражения 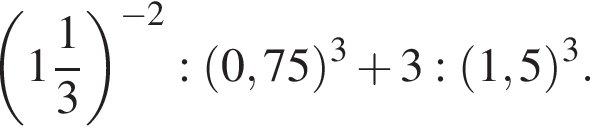
Величины a и b являются прямо пропорциональными. Используя данные таблицы, найдите неизвестное значение величины a.
| a | 1,3 | |
| b | 112 | 9,1 |
На координатной плоскости изображен параллелограмм ABCD с вершинами в узлах сетки (см.рис.). Длина диагонали AC параллелограмма равна:
Число 185 является членом арифметической прогрессии 5, 9, 13, 17, ... Укажите его номер.
Величины a и b являются прямо пропорциональными. Используя данные таблицы, найдите неизвестное значение величины a.
| a | 1,7 | |
| b | 102 | 5,1 |
На рисунке изображены развернутый угол AOM и лучи OB и OC. Известно, что ∠AOC = 127°, ∠BOM = 153°. Найдите величину угла BOC.

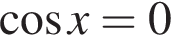 или когда
или когда 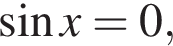 т. е. при
т. е. при 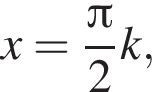 где
где 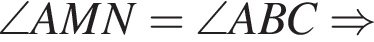
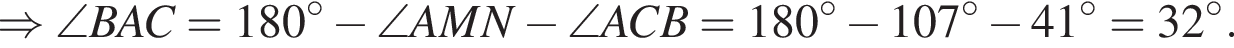
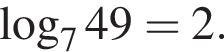
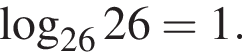
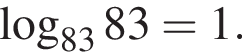
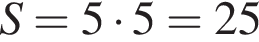 см2.
см2.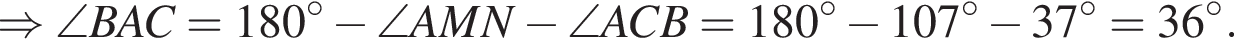
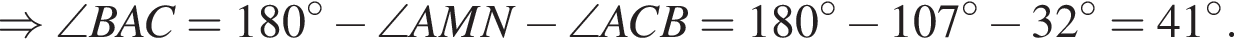

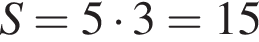 см2.
см2.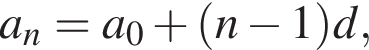 где d — разность арифметической прогрессии. Коэффициент перед n и есть разность арифметической прогрессии, он равен 6.
где d — разность арифметической прогрессии. Коэффициент перед n и есть разность арифметической прогрессии, он равен 6. равна 360°, поэтому четвертый угол равен 150°. Углы 1 и 3, 2 и 4 — вертикальные, следовательно, они равны. Смежные углы в сумме 180°, следовательно, меньший угол равен 30°.
равна 360°, поэтому четвертый угол равен 150°. Углы 1 и 3, 2 и 4 — вертикальные, следовательно, они равны. Смежные углы в сумме 180°, следовательно, меньший угол равен 30°.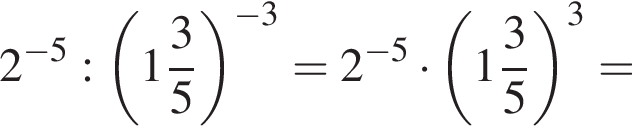
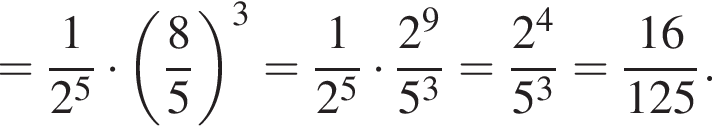
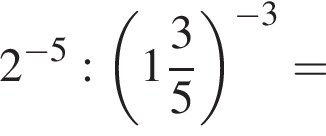
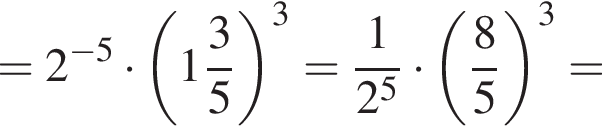
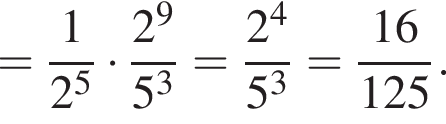

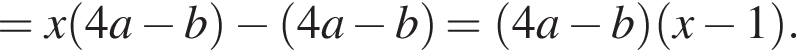

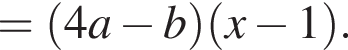
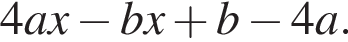
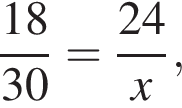 где x — неизвестное число.
где x — неизвестное число.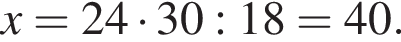
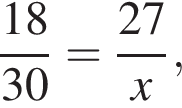 где x — неизвестное число.
где x — неизвестное число.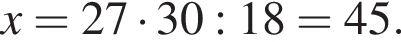
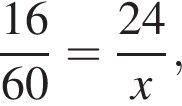 где x — неизвестное число.
где x — неизвестное число.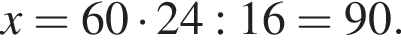

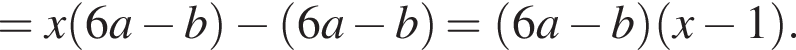

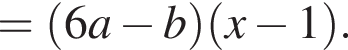
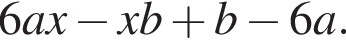
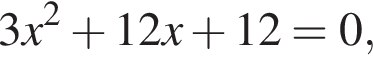 дискриминант равен нулю, значит, корень есть.
дискриминант равен нулю, значит, корень есть.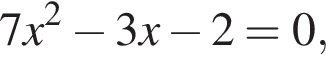 дискриминант больше нуля, значит, корни есть.
дискриминант больше нуля, значит, корни есть.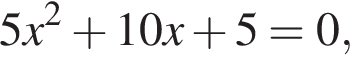 дискриминант равен нулю, значит, корень есть.
дискриминант равен нулю, значит, корень есть.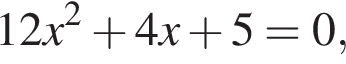 дискриминант меньше нуля, значит, корней нет.
дискриминант меньше нуля, значит, корней нет.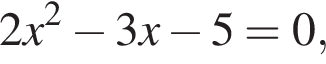 дискриминант больше нуля, значит, корни есть.
дискриминант больше нуля, значит, корни есть.
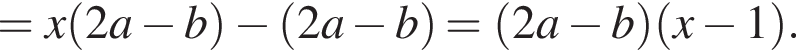

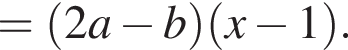
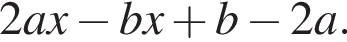
 Известно, что
Известно, что 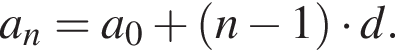 Тогда:
Тогда: 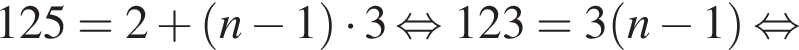
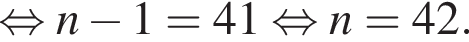
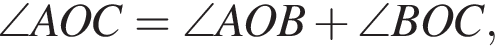
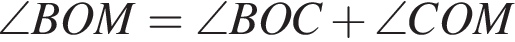 и
и  Таким образом:
Таким образом:
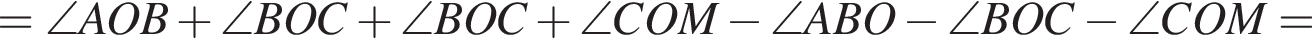
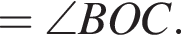
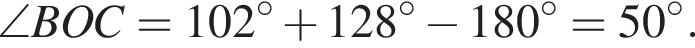
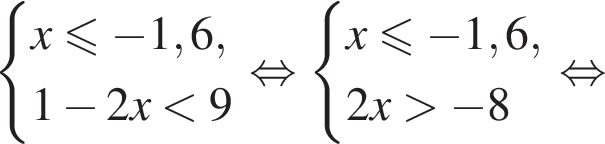
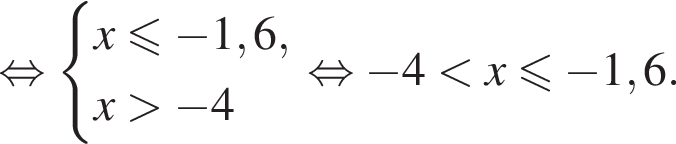
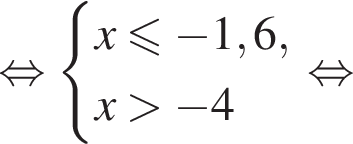
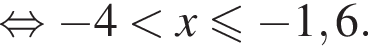
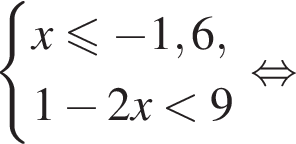
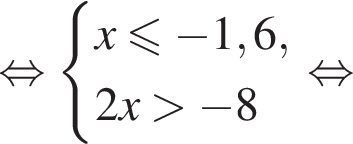
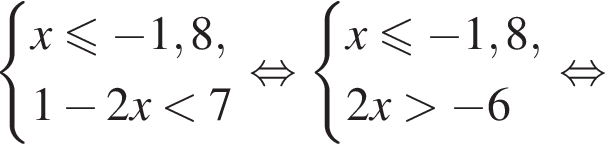
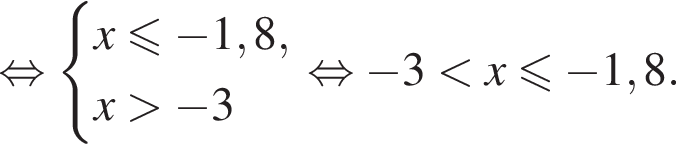
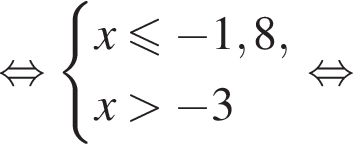
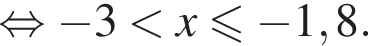
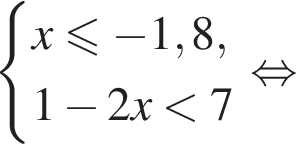
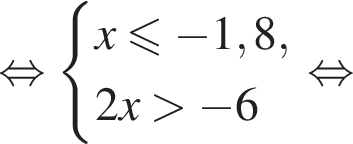
 Известно, что
Известно, что 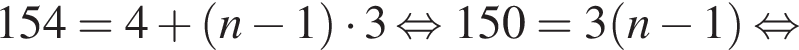

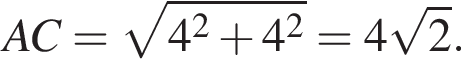
 Известно, что
Известно, что 
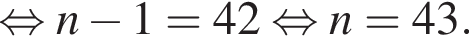
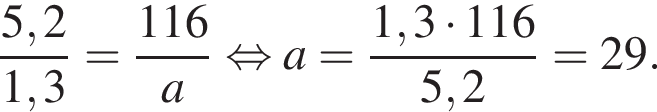
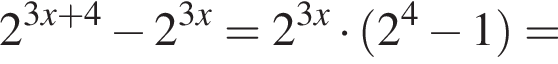
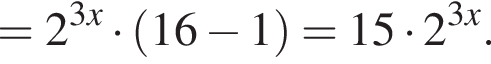
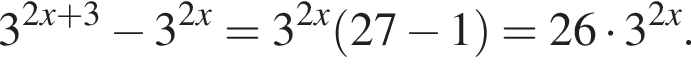
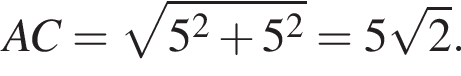
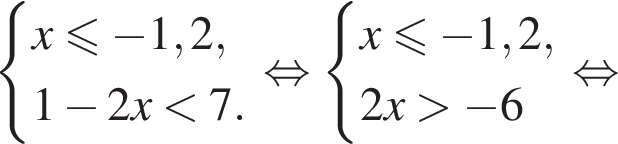
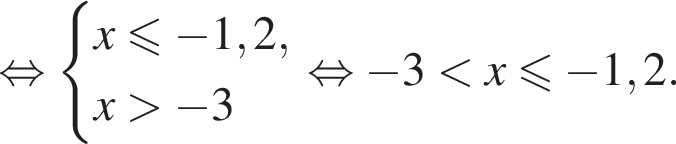
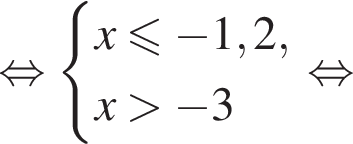
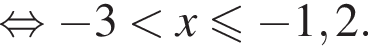
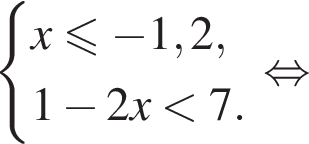
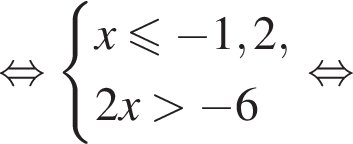
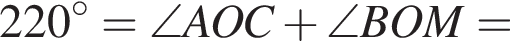

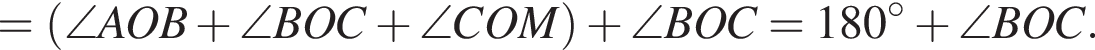



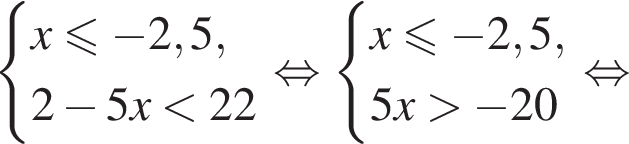
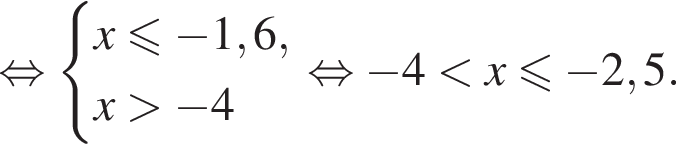
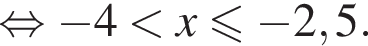
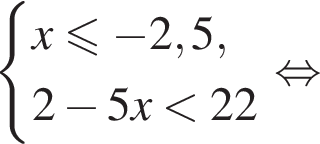
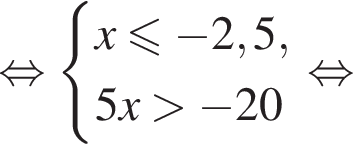
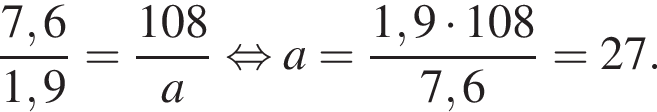

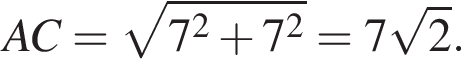
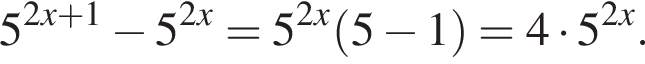
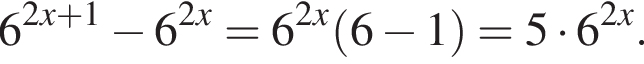

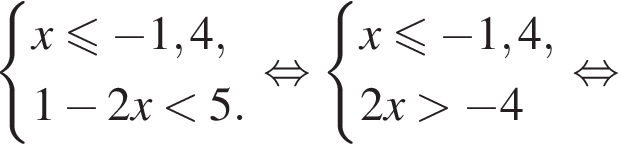
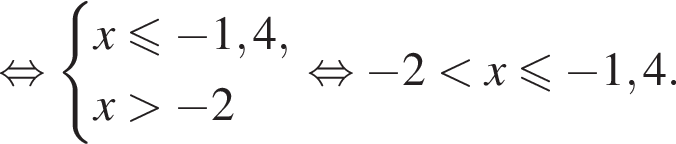
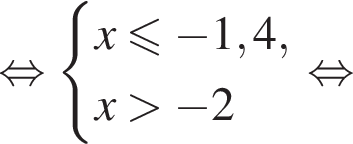
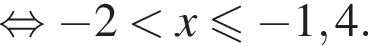
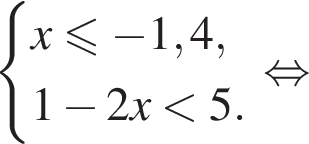
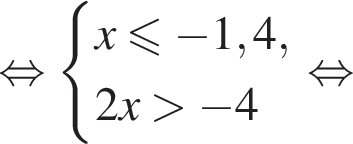
 Известно, что
Известно, что 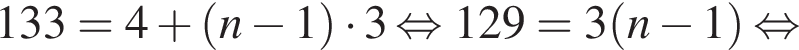
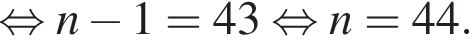
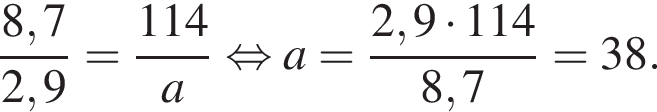
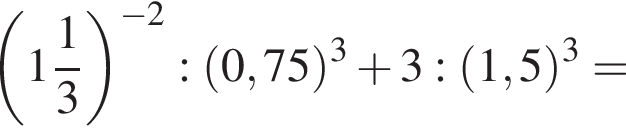

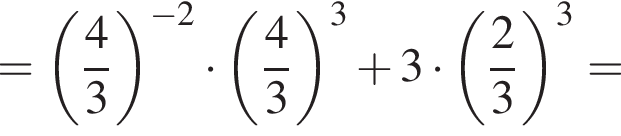
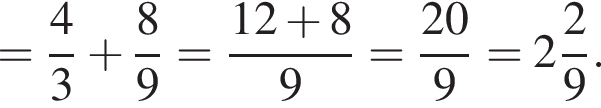
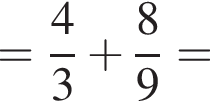
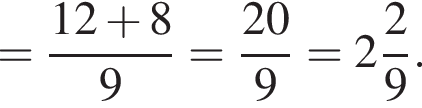
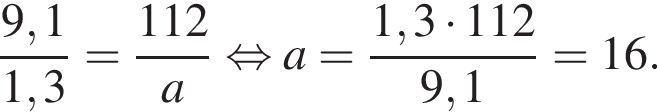
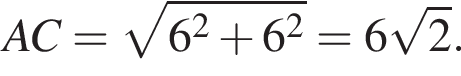
 Известно, что
Известно, что